Geometry #6 이미지 투영
Image Geometry
지금까지의 내용을 종합하여 3D 월드좌표에서 2D 픽셀좌표로 변환 관계 즉, 이미지가 형성되는 과정을 정리하겠다.
1.원근 투영 변환(Perspective Projection Transformation)
먼저 3D에서 2D로의 투영 변환행렬을 살펴보겠다.
투영변환은 3차원 공간에 있는 점을 이미지 평면에 투영시키는 변환인데, 투영변환을 모델링하는 방법에는 크게 2가지가 있다.
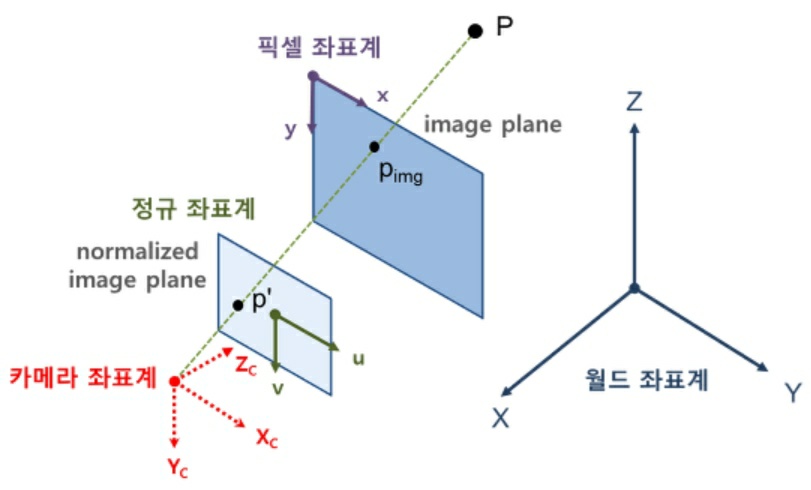
하나는 위 그림처럼 투영 기준점(projection reference point)을 좌표계의 원점으로 잡고(카메라 좌표계가 원점) 이미지 평면(정규 좌표계가 있는 평면)을 전방 Zc = d(d는 이미지 평면과의 거리로 추측)에 두는 경우(이미지 평면이 Zc 앞에 있다)이고 다른 하나는 투영시킬 이미지 평면을 좌표계 원점에 위치시키고 투영 기준점을 Zc = -d에 잡는 경우(이미지 평면이 Zc 뒤에 있다)이다.
먼저 첫번째 경우(위 그림의 경우)처럼 투영 기준점을 윈점으로 잡은 경우 3차원 상의 점 P를 p’로 투영시키는 변환 행렬은 다음과 같다(Homogeneous 표현).
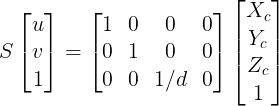
즉, 투영 평면이 Zc = d일 경우 (Xc, Yc, Zc, 1)은 (d * Xc/Zc, d * Yc/Zc, 1)로 투영 된다.
=(Xc, Yc, Zc)이고 위 변환행렬의 결과를 마지막 요소값이 1이 되도록 나누어준 결과이다
다음으로 투영평면이 Zc = 0이고 투영기준점을 (0, 0, -d)인 경우의 투영 변환 행렬은 다음과 같다.
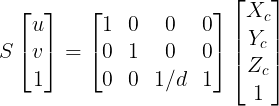
이 경우 (Xc, Yc, Zc, 1)은 (d * Xc/(Zc+d), d * Yc/(Zc+d), 1)로 투영된다.
이 외에도 투영변환을 표현하는 방법은 다양하다, 여기서는 첫번째 식을 기준으로 Zc = d로의 투영변환을 다음과 같이 표현하겠다.
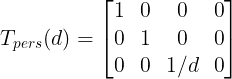
2.이미지 투영 모델
월드 좌표계 상의 한 점(X, Y, Z)를 픽셀 좌표계의 이미지 평면 상의 점 (x, y)로 변환시키는 행렬을 H라 하면 그 관계식은 다음과 같다.
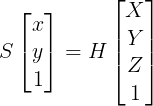
여기서 H는 3*4 행렬로서 다음과 같이 분해하여 표현할 수 있다.

위 식에서 [R|t]는 월드 좌표계를 카메라 좌표계로 바꾸는 Rigid 변환 행렬이고 Tper(1)는 카메라 좌표계 상의 3D 좌표를 정규 이미지 평면에 투영시키는 Projection 행렬(Tper(1)에 1은 d=1인 Zc=1를 의미하고 평면으로의 투영변환 즉, 정규 이미지 평면에 투영을 뜻한다), K는 카메라 내부 파라미터 행렬로 정규 이미지 좌표를 픽셀 좌표로 바꾸어 준다.
위 식에서 투영변환 Tper과 Rigid 변환 [R|t]를 하나로 합치면 다음과 같이 간단한 표현식이 된다.
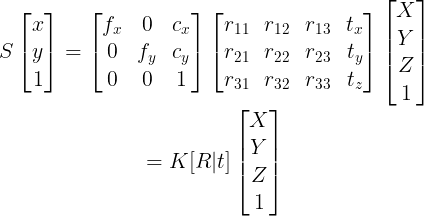
식(1)
이 때, 앞부분 K를 내부 카메라 행렬이라 부르고, 내부 파라미터를 나타내고, [R|t]는 카메라 외부 파라미터를 나타낸다.
위 식에서 카메라 내부 파라미터 행렬인 K에 대한 기하학적 해석이 직관적이지 않은 문제가 있다. 왜냐하면 실제 투영은 가상의 정규 이미지 평면이 아닌 초점거리 f인 이미지 평면에 투영되기 때문이다. 따라서 실제로는 투영변환이 Zc = f 평면으로의 투영인 Tper(f)가 되어야 하므로 K는 물리적인 metric 좌표 단위를 픽셀 좌표계 단위로 변환시켜주는 변환 행렬이 되어야 한다. 식으로 나타내 보면 다음과 같다.
 식(2)
식(2)
위 식에서 f는 초점거리(카메라 좌표계의 원점과 이미지 센서와의 거리), sx, sy는 이미지 센서의 metric 단위를 x, y 픽셀 단위로 바꿔주는 일종의 스케일 요소이다.
Tpers(f)가 처음 설명할 때의 식과는 다른 형태로 표현 했는데 Homogeneous좌표이기 때문에 표현만 다를뿐 같은 변환이다.
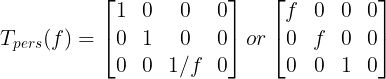
결과적으로 식(1)과 식(2)을 비교해 보면 단지 sxf를 fx, syf를 fy로 표현한 것임을 알 수 있다. 하지만 일반적으로 사용되는 카메라 모델 표현은 식(1)을 사용한다.
그리고 식(1)을 보면 알겠지만 __영상왜곡__은 고려하지 않았다. 영상왜곡까지 고려하려한다면 투영변환과 내부 파라미터 변환 사이에 왜곡모델이 들어가야 한다.
즉, nomalized 이미지 평면에 투영된 좌표 (u, v)에 대해 왜곡 파라미터를 적용한 후 K(내부 파라미터)를 통해 픽셀 좌표계로 변환해야 한다.

Leave a comment