Geometry #5 3D 변환
컴퓨터 비전에서 주로 다루는 3D 변환은 회전과 평행이동 뿐이다(=Rigid변환).
1.변환행렬
회전축에 따른 표현방법
1-1. 3차원 공간의 점 (X, Y, Z)를 X축, Y축, Z축을 중심으로 θ 라디안(radian) 회전 시키는 행렬을 각각 Rx(θ), Ry(θ), Rz(θ)라 하면 이들은 다음과 같다.
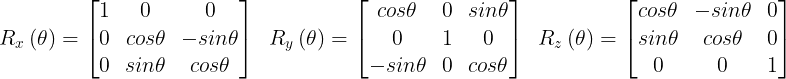
이 때, 회전방향은 아래 그림과 같이 각 축에 반시계 방향이다.(오른손 엄지를 축의 방향으로 뒀을 때 말아쥔 손가락이 회전 방향)
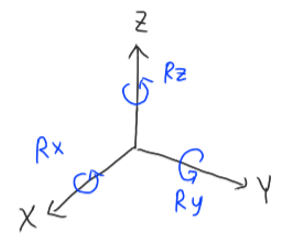
위 3 방향의 기본 회전변환을 조합하면 임의의 3D 표현을 표현할 수 있다.
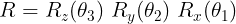
1-2. 좌표축이 아닌 임의의 단위벡터 u = (ux, uy, uz)를 회전축으로 한 회전변환 행렬은 다음과 같다(단, ux^2 + uy^2 + uz^2 = 1)
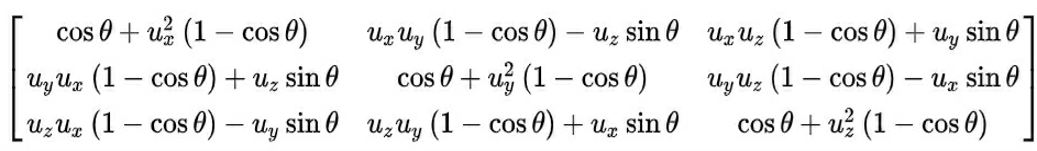
회전변환 R, 평행이동 t = [tx, ty, tz]^T를 이용한 일반적인 3D 변환식(Rigid 변환)은 다음과 같다.
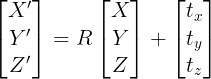
2D 변환과 마찬가지로 3D 변환에서도 homogeneous 좌표를 사용하면 다음과 같이 회전변환과 평행이동을 하나의 변환행렬로 즉, 선형변환 형태로 표현할 수 있다.
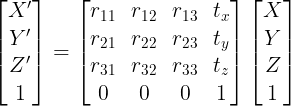
참고로 위키피디아에 보면 어떤 행렬 R이 회전변환 되기 위한 필요충분 조건은 R^T = R^-1(전치행렬과 역행렬이 같다), det(R) = 1 이라 한다(det는 행렬식).
2.변환관계 구하기
예를 들어 3D 공간에서 움직이는 비행기의 임의의 두 지점 사이의 변환 관계를 구하는것을 목표로 한다고 하자. 이 변환관계를 회전변환과 평행이동만으로 표현할 수 있다.
2-1. 회전변환 구하기
크기가 같은 임의의 두 벡터 u = [x, y, z]^T, u’ = [x’, y’, z’]^T가 있을 때, u를 u’로 이동시키는 회전변환은 다음과 같이 구할 수 있다.
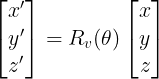
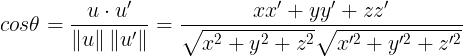

내적을 이용하여 cos세타와 sin세타를 구하는 과정
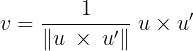
외적으로 회전축인 법선벡터를 구하는 과정
θ는 두 벡터 u, u’ 사이의 사잇각이며 벡터의 내적을 이용하여 쉽게 구할 수 있다. 회전축은 두 벡터 u, u’에 의해 결정되는 평면(=꼬인 상태x)에 수직인 벡터 즉, 벡터의 외적을 이용하면 된다. 이렇게 구한 회전각 θ와 회전축 단위벡터 v를 앞에 나온 단위벡터를 회전축으로한 회전변환 행렬의 식에 대입하여 원하는 회전변환 행렬을 구할 수 있다.
2-2. Rigid 변환 구하기
회전 뿐 아니라 평행이동까지 포함한 문제로 확대하여 본다.
3차원 공간에서 물체의 위치 및 방향을 유일하게 결정하기 위해서는 최소 3개의 점이 있어야 한다(최소 3개가 있어야 평면(=3차원 물체)을 결정할 수 있으므로).
마찬가지로 3차원 공간에서 움직이는 물체의 위치 관계를 표현하기 위해서는 3개의 매칭쌍만 있으면 된다. 즉 3D에서 Rigid 변환을 결정하기 위해서는 3개의 매칭쌍을 필요로 한다.
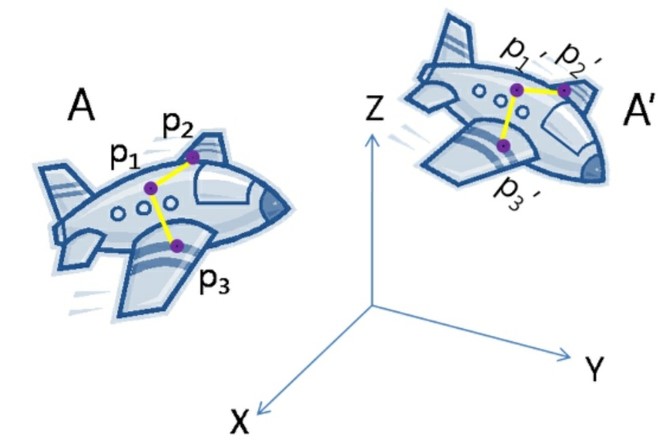
위 비행기 그림을 예로 들어 Rigid 변환을 구해보면 위치 A에서의 점을 (x, y, z)=(p1, p2, p3) 위치 A’에서의 점을 (x’, y’, z’)=(p1’, p2’, p3’)라고 할때, 변환과정을 간략히 살펴보면
1) p1이 원점에 오도록 평행이동 시킨다
2)A’의 방향과 일치하도록 평행이동 시킨 A를 회전시킨다
3)p1을 p1’까지 평행이동 시킨다
이렇게 된다. 회전을 시킬 때 2번의 회전이 필요한데 한번은 벡터 p1p2가 벡터 p1’p2’와 일키하게 회전하는것(R1)이고 나머지 한번은 p3와 p3’가 일치하게 회전을 시킨다(R2)(원점을 중심으로 회전하는것이기 때문에 한번의 회전으로는 불가능하다). 식으로 나타내면 다음과 같다.
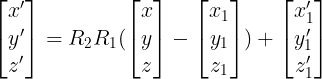
R1은 위의 회전변환 구하는 식을 사용하여 구할 수 있지만 R2를 구하는게 어렵다.

Leave a comment