Geometry #2 Homogeneous Coordinate
1.동차 좌표를 사용하는 이유
동차 좌표계를 사용하면 무한대의 개념을 활용할 수 있다. 이는 컴퓨터 그래픽 분야에서 필요한 기하학적 개념과 계산을 쉽게 할 수 있다.
-> affine 변환이나 perspective(projective)변환을 하나의 단일 행렬로 표현할 수 있다.
(무한대 : 무한대의 개념은 두 실수를 활용하여 나타낼 수 있다. 예를들어, 두 실수 a, w가 있을 때 a/w 에서 w값을 0에 가까워 지면 a/w는 무한대에 가까워진다)
2.동차 좌표계
위에 내용 처럼 무한대는 한쌍의 실수로 나타낼 수 있다. 이를 xy 평면에 적용하면 (x,y) -> (x/w, y/w)로 나타낼 수 있다.
이와 같은 2차식에서 x,y를 x/w, y/w로 치환하고 계수들을 w제곱을 곱하여 정리해주면
위 식을 보면 모든 항들의 차수가 같다. 즉 균일(Homogeneous)하다. 이래서 동차좌표계라고 한다. 좌표 표기는 (x, y, w)로 한다.
3.카메라 좌표계와 동차 좌표계의 관계
정규 이미지 평면에서의 점 p’ = (u, v) 에 대한 동차 좌표 표현은 (u, v, 1)이다. 그런데 이 점을 카메라 좌표계에서 봤을 때의 3D 좌표도 (u, v, 1)이다. 카메라 좌표계 입장에서 투영선 상에 있는 점들의 3D좌표는 (wu, wv, w)가 된다. 이것은 (u, v)의 일반적인 동차좌표 표현과 일치한다.
이러한 관점에서 보면 동차 좌표(x, y, w)에서 일반 좌표(x, y)로 변환하는 과정은 projection, 일반좌표에서 동차 좌표로 변환하는 과정을 inverse projection과정이라고 할 수 있다.
4.사영 기하학
-사전적 의미 : 투영 변환에 대해 불변인 기하학적인 특성을 연구하는 것
사영 기하학에서 두 동차 좌표 (x, y, 1), (2x, 2y, 2)는 동일한 한 점 (x, y)로 투영되기 때문에 같은 점이라고 할 수 있다. 또한 길이와 각도가 보존 되지 않고, 유클리드 기하과 달리 평행성도 보존 되지 않는다. 보존되는 것은 type이다. type이 보존된다는것은 직선은 직선, 곡선은 곡선으로 투영된다는 것이다.

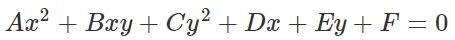

Leave a comment